axiomatiser

axiomatiser

axiomatiser [ aksjɔmatize ] v. tr. <conjug. : 1>
• v. 1935; de axiomatique
♦ Organiser sous forme axiomatique par un système déductif ou par la formalisation. — P. p. adj. Théorie partiellement axiomatisée.

● axiomatiser verbe transitif Soumettre quelque chose à une axiomatisation. Expliciter les termes non définis et les postulats non démontrés sur lesquels repose une théorie mathématique déductive.

⇒AXIOMATISER, verbe trans.
Vocab. sc. et lang. abstr. ou philos. Organiser une théorie ou toute construction de l'intelligence sous forme d'axiomes ou de principes :
• 1. ... on axiomatise ce que déjà l'on connaît. On axiomatise pour bien administrer la rigueur de la connaissance. L'axiomatique est une reprise, jamais un vrai départ.
G. BACHELARD, Le Rationalisme appliqué, Paris, P.U.F., 1962, p. 28.
• 2. Aussi bien la société n'est-elle pas seulement une structure objective; la constitution politique axiomatise un certain état des rapports humains, et l'on ne peut modifier les rapports entre hommes qu'en prenant acte de ce qu'ils sont.
G. GUSDORF, Traité de métaphys., Paris, Armand Colin, 1956, p. 446.
— LOG. et MATH. MOD. Axiomatiser une théorie déductive. Synon. formaliser, symboliser. Cf. axiome et axiomatique :
• 3. On peut assurément veiller à ajuster la logique qu'on axiomatise sur celle-là même dont on se sert pour l'axiomatiser, à faire en sorte, autrement dit, que la logique opératoire vienne s'appliquer sur la logique axiomatisée, comme l'un de ses modèles possibles.
R. BLANCHÉ, L'Axiomatique, Paris, P.U.F., 1959, p. 64.
Rem. 1re attest. 1949 (d'apr. ROB. Suppl. 1970); dér. de axiomatique, suff. -iser. Largement attesté ds les dict. gén. du XXe s. à partir de Lar. encyclop. de plus en plus fréq. dans le vocab. de la ling., de la log. et des math. modernes.
PRONONC. :[].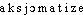
BBG. — FOULQ.-ST-JEAN 1962.

axiomatiser [aksjɔmatize] v. tr.
ÉTYM. 1935, p. p., in Actes du congrès international de philosophie des sciences; de axiomatique.
❖
♦ Didact. Organiser sous forme axiomatique, par un système déductif ou par la formalisation.
0 (…) il existe aussi « en deçà » des frontières que la logique aurait pour tâche de formaliser ou d'axiomatiser et qui consisterait non pas en la pensée consciente du sujet, mais en ses structures opératoires.
J. Piaget, Épistémologie des sciences de l'homme, p. 226 (1970).
♦ Au p. p. || Théorie partiellement axiomatisée.
❖
DÉR. Axiomatisable, axiomatisation.

Encyclopédie Universelle. 2012.

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • axiomatisation — [ aksjɔmatizasjɔ̃ ] n. f. • 1936; de axiomatiser ♦ Didact. Action d axiomatiser; état de ce qui a été axiomatisé. ⇒ formalisation. L axiomatisation d une science. « L axiomatisation [est] l acte mental qui aboutit à la création du schéma abstrait …   Encyclopédie Universelle

  • Theorie des ensembles de von Neumann-Bernays-Godel — Théorie des ensembles de von Neumann–Bernays–Gödel La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec… …   Wikipédia en Français

  • Theorie des ensembles de von Neumann–Bernays–Godel — Théorie des ensembles de von Neumann–Bernays–Gödel La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec… …   Wikipédia en Français

  • Théorie NBG — Théorie des ensembles de von Neumann–Bernays–Gödel La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec… …   Wikipédia en Français

  • Théorie des classes — Théorie des ensembles de von Neumann–Bernays–Gödel La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec… …   Wikipédia en Français

  • Théorie des ensembles de Von Neumann–Bernays–Gödel — La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec axiome du choix (et avec les mêmes variantes… …   Wikipédia en Français

  • Théorie des ensembles de von Neumann-Bernays-Gödel — Théorie des ensembles de von Neumann–Bernays–Gödel La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec… …   Wikipédia en Français

  • Théorie des ensembles de von Neumann–Bernays–Gödel — La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec axiome du choix (et avec les mêmes variantes… …   Wikipédia en Français

  • Théorie des ensembles de von neumann–bernays–gödel — La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec axiome du choix (et avec les mêmes variantes… …   Wikipédia en Français

  • formaliser — (se) [ fɔrmalize ] v. pron. <conjug. : 1> • 1539; de formel, d apr. lat. formalis ♦ Être choqué d un manquement à la politesse formelle, au savoir vivre, aux conventions sociales. ⇒ s offenser, s offusquer, se piquer, se vexer. Se… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”